Cournot Model

Assumptions

• 2 firms are competing with each other (oligopoly)
• Homogeneous good (no product differentiation)
• Simultaneous output decisions (the firms decide how much to produce at the same time)
• Each firm treats the output level of its competitor as fixed when deciding how much to produce
• Full information and rationality

Example: Hotel

A hotel owner chooses how many rooms to build and then sets his price based on the total amount of accommodation available in the resort and the demand level

Profit Maximization in the Cournot Model

$$P=a-b{Q}_{\text{T}}\text{ ; }{Q}_{\text{T}}=Q_1+Q_2\text{ and }M{C}_1=c_1$$ $$\begin{array}{rl}{\pi }_1(Q_1,Q_2)& =R-C\\ & =P{Q}_{1-C}\\ & =(a-b{Q}_T)Q_1-c_1{Q}_1-F_1\\ & =(a-b{Q}_1-b{Q}_2)Q_1-c_1{Q}_1-F_1\\ & =a{Q}_1-b{Q}_1^2-b{Q}_2{Q}_1-c_1{Q}_1-F_1\end{array}$$

→ this maximizes $q_1$ when setting derivative to 0:

$$\frac{\delta {\pi }_1(Q_1,Q_2)}{\delta Q_1}=a-2b{Q}_1-b{Q}_2-c_1=0$$

$a-2b{Q}_1-b{Q}_2$ is $M{R}_1$ in the above formula $-c_1$ is $-M{C}_1$ in the above formula

$$Q_1^{\ast }=\frac{a-b{Q}_2-c_1}{2b}$$

The optimal output is a function of the output of the other firm! The more Firm 2 produces, the less Firm 1 will produce

Firm 1’s output decision

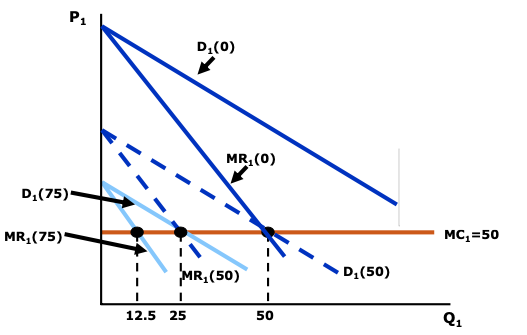
• If Firm 1 thinks that Firm 2 will produce nothing, then the demand curve for Firm 1, $D_1(0)$, is equal to the market demand curve.
• If Firm 1 believes that Firm 2 will produce 50 units, the demand curve facing Firm 1 will move 50 units to the left.
• If Firm 1 thinks that Firm 2 will produce 75 units, the demand curve facing Firm 1 will move left by 75 units. $\Downarrow$
• The output of Firm 1 depends on the output decision of Firm 2: the optimal output of Firm 1 decreases as the optimal output of Firm 2 increas<es.

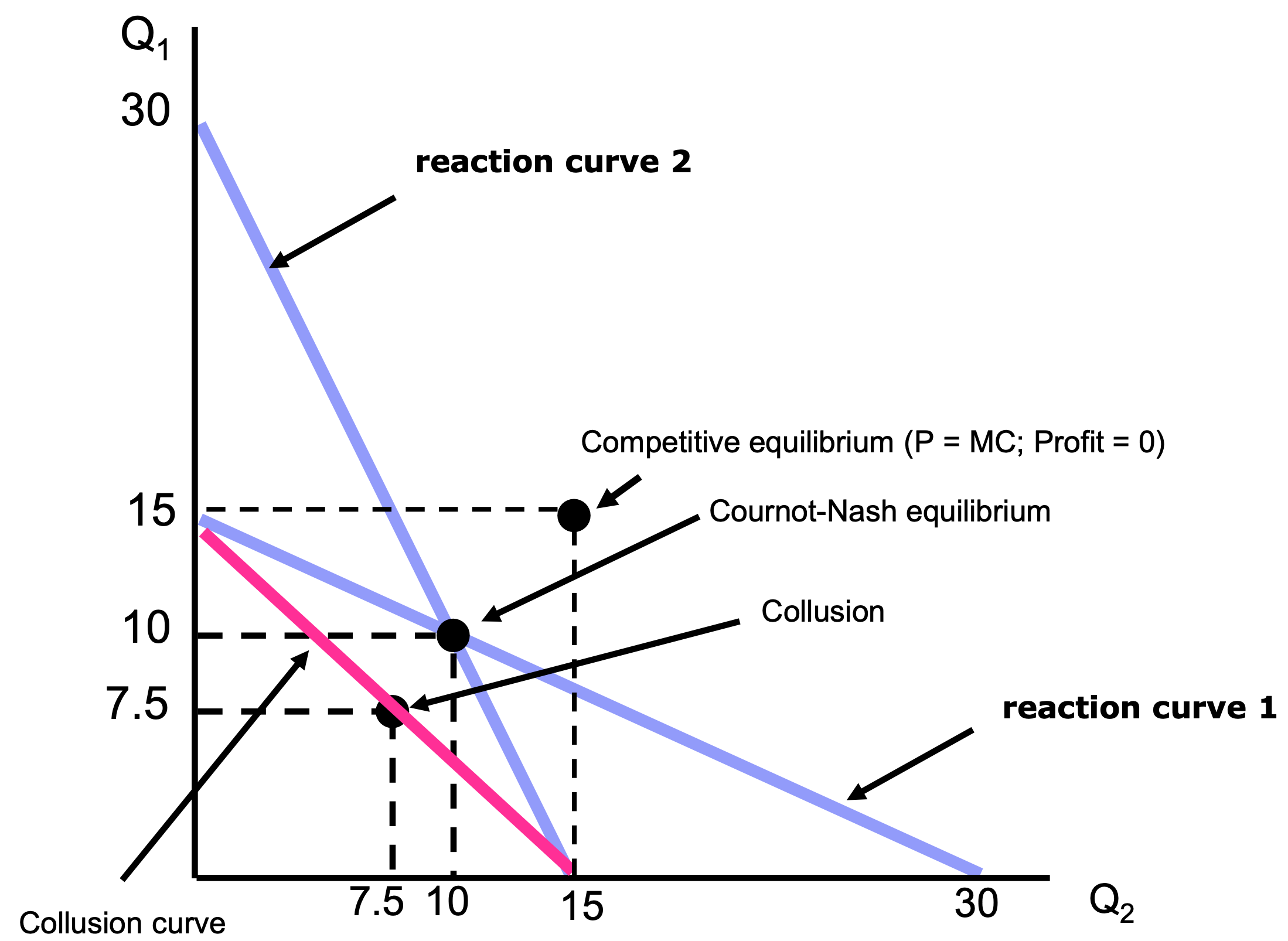
Reaction Function

• Firm 1’s reaction curve shows how much it will produce as a function of how much it thinks Firm 2 will produce.
• Firm 2’s reaction curve shows its output as a function of how much it thinks Firm 1 will produce.
• Reaction functions show the relationship between a firm‘s profit maximizing output and the amount it thinks its competitor will produce.

Important

In the Cournot equilibrium, each firm correctly assumes the amount that its competitor will produce and thereby maximizes its own profits. Therefore, neither firm will move from this Nash Equilibrium.

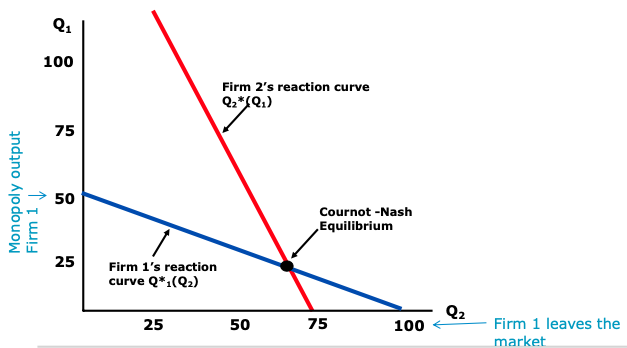
Example: Extreme Duopoly

? similar example in the Stackelberg Model a) Two firms are competing in a market with the linear inverse demand function $P=30-Q$ with $Q=Q_1+Q_2$. Calculate the profits of two firms, assuming marginal costs of zero.

$P=30-Q$ $C_1=C_1=0$ → ${\Pi }_1(q_1,q_2)=(30-(q_1+q_2))q_1\to \text{max }{q}_1$ $30-q_1-q_2-q_1=0$ $q_1=\frac{30-q_2}{2}$

→ ${\Pi }_2(q_2,q_1)=(30-(q_1+q_2))q_2\to \text{max }{q}_2$ $q_2=\frac{30-q_1}{2}$ BR (best response) of firm 2

→ Nash Equilibrium: $q_1^{\ast }=q_2^{\ast }=0$ ${\Pi }_1^{\ast }={\Pi }_1^{\ast }=100$

b) Calculate the profits of the firm, assuming collusion. If the firms collude, they are maximizing joint profits and acting like a monopolist.

$(30-Q)Q\to \text{max }Q$ $30-2Q=0$ $Q=15$ ${\Pi }^{\ast }=225$