🪴 Maixnor WU

Game Theory

Nov 04, 20254 min read

Definition

Framework about strategic, interactive situations

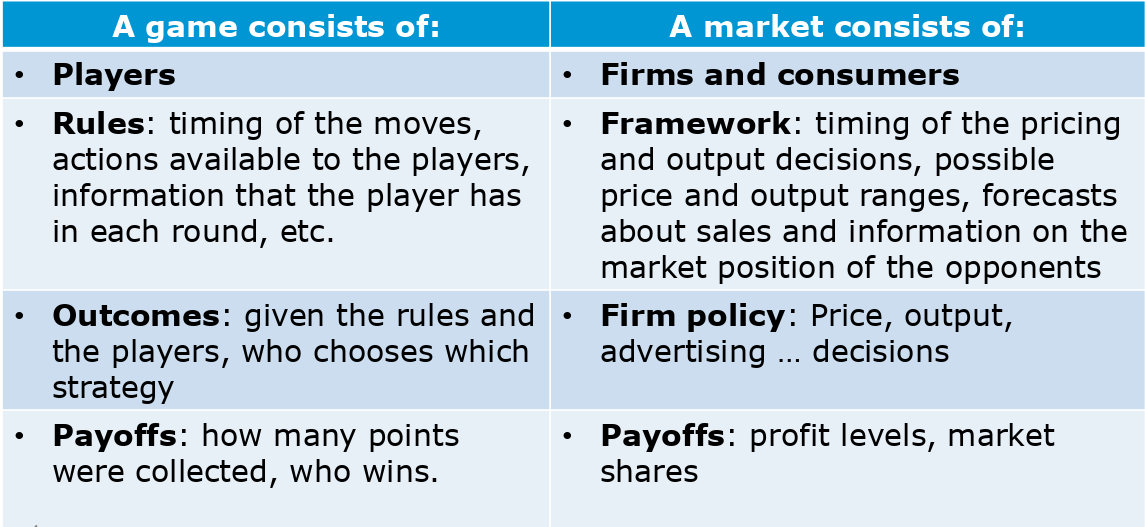
Info

Game … interaction between multiple agents which effect the others Player … actor, agent in this interaction

History

Nobel Prizes

Games and Competition

  • sequential or constant game
  • game plan
    • each player has a predefined action/reaction trees
    • imagine chess with pre-planned moves (e.g. chess openings)
    • no game plan for chess (too many options)

Assumptions

  • every actor understands the payoffs of the game
  • players have preferences
  • Rationality - all players are rational → maximize payoffs
  • complete knowledge
    • all information is available to everyone
    • everyone knows that all information is known by everyone
  • players have unlimited reasoning and calculation ability

Criticism

  • players are not rational
  • not all players have all knowledge

Nash Equilibrium

  • Nash Equilibrium
  • for all players the utility has been maximized given the actions of the other players
    • i.e. sticking to the current (best) option, since every other option is inferior for every player
  • there can be more than one nash equilibrium, but there must always be at least one
  • mathematical notation

Payoff Matrix

Types of Games

  • static/simultaneous vs dynamic/sequential
  • pure-strategy equilibrium vs mixed-strategy equilibrium
  • complete information vs incomplete information

Solutions of a Static Game

  • find the possible strategies of all players
  • determine the payoffs
  • find optimal strategies of all players
  • reach Nash Equilibrium

Strategies

Multiple Equilibria - Battle of the Sexes

  • when 2 strategies are exactly opposite to one another
  • combination of all payoffs are equally beneficial
  • multiple predictions are valid
  • actual solution is outside of scope of analysis
    • i.e. depending on actions of actors the system will reach any Nash Equilibrium
  • 2nd order decision
    • if there are multiple equilibria i.e. equally well for me
    • then I can choose the equilibrium which hurts other player(s) the most
  • Football vs Opera Game

Prisoners Dilemma

Maximin Strategy

  • no complete rationality or not fully informed players
  • even tho a Nash Equilibrium may be possible there is still the risk that the other player does not follow the optimal strategy
    • when e.g. an investment is risky then it might be better to leave the dominant strategy and choose the risk-averse strategy
    • risk-averse strategy → maximin strategy
  • asking: “what is the worst thing that can happen?” for all possibilities
    • maximin strategy → choose the best worst thing

No Solution - Mixed Strategy

Solutions of a Dynamic Game

Repeated Games

Finite Games

  • game is played a number of times
  • last-move optimization → state at last move will be nash equilibrium
  • deviations from equilibrium are only possible, if the deviation is not punished in the next turn/state of the game
  • First Mover Advantage can be meaningful

Info

Infinite Games

  • a game is not just played once, but infinitely many times
    • i.e. there is no last move → no last-move optimization
  • genuine repetition dynamics can flourish
    • e.g. cooperation
  • Discounting for future earnings
  • First Mover Advantage only limited

Tit-for-Tat Strategy

  • I do what you did to me last time
  • this can sustain collusion for long times, even when there are disruptions
  • Stackelberg Model

Grim Trigger Strategy

  • I will collude, until you cheat only once
  • after the first cheat, I will always compete with you
  • this can sustain collusion for long times, until there is any disruption

Goals of Firms

Which actions give me an edge in the market?

  • make entry unattractive → Market Entry Barriers
  • hurting competitors
    • reduce output
    • stop producing entirely (exit market)
  • setting threats
    • empty threats
      • threats against player with dominant strategy are futile
      • they will always be on top of others, you can only reduce the overall social optimum
  • First Mover Advantage - if present

Types of Games

Backlinks